The cuts were made for the 10^4 and 10^7 periods and the limit of the eccentricity was set to 0.3 (grid-size Δe = 0.05), the mass ratios were set to μ = 0.01 (grid-size Δμ = 0.001).
The limit between a brown dwarf and a GG is incidental from the following:
The minimum mass required to cause substantial fusion is approximately 13 Jupiter masses (read more at the International Astronomical Union IAU or Gibor Basri & Michael E. Brown 2005).
In Figs. 3 and 4 we present the size of the stable area (given in [AU^2]). The grey-scale of the stable area goes from 0.05 to 0.5 [AU^2]. To visualise how large the stable area around an extrasolar Lagrangian equilibrium point could be, we calculated the area inside the orbit of Mercury and got an area of 0.43 [AU^2].

Fig. 4 shows Finger-like structures which are separated by high-order resonances between the libration periods of the massless body. We marked the 2:1 and the 3:1 resonances, which are pointed out in the work of Érdi et al. (2007b). Concerning the further mentioned limit of a brown dwarf, we focused our investigations between 1 and 10 Jupiter masses (Fig. 4) and extended the integration time from 10^4 periods up to 10^7 periods. 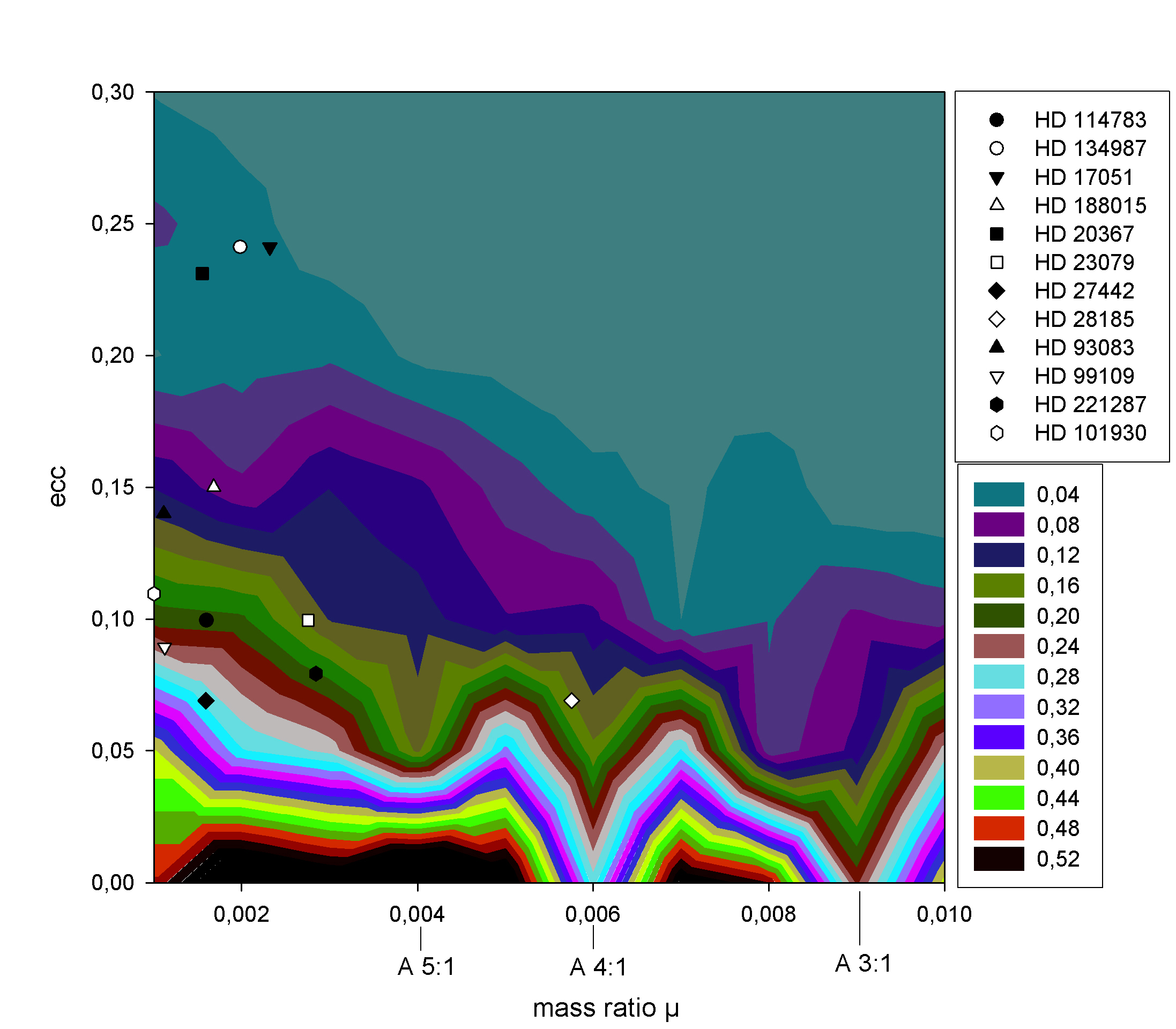The catalogue was normalised to 1 AU (shown in Fig. 2), because in most cases the HZ is close to 1 AU for G-stars. If the GG is not at 1 AU distance to the central star, it is necessary to adapt the stable area. Thus we have to recalculate values of the stable area from the catalogue to that of the real system. This is only a simple scale transformation: the axes of the stable area (a, λ) are scaled to the unit circle at 1 AU and can be easily recalculated by dividing them by the semimajor axis of the real system.

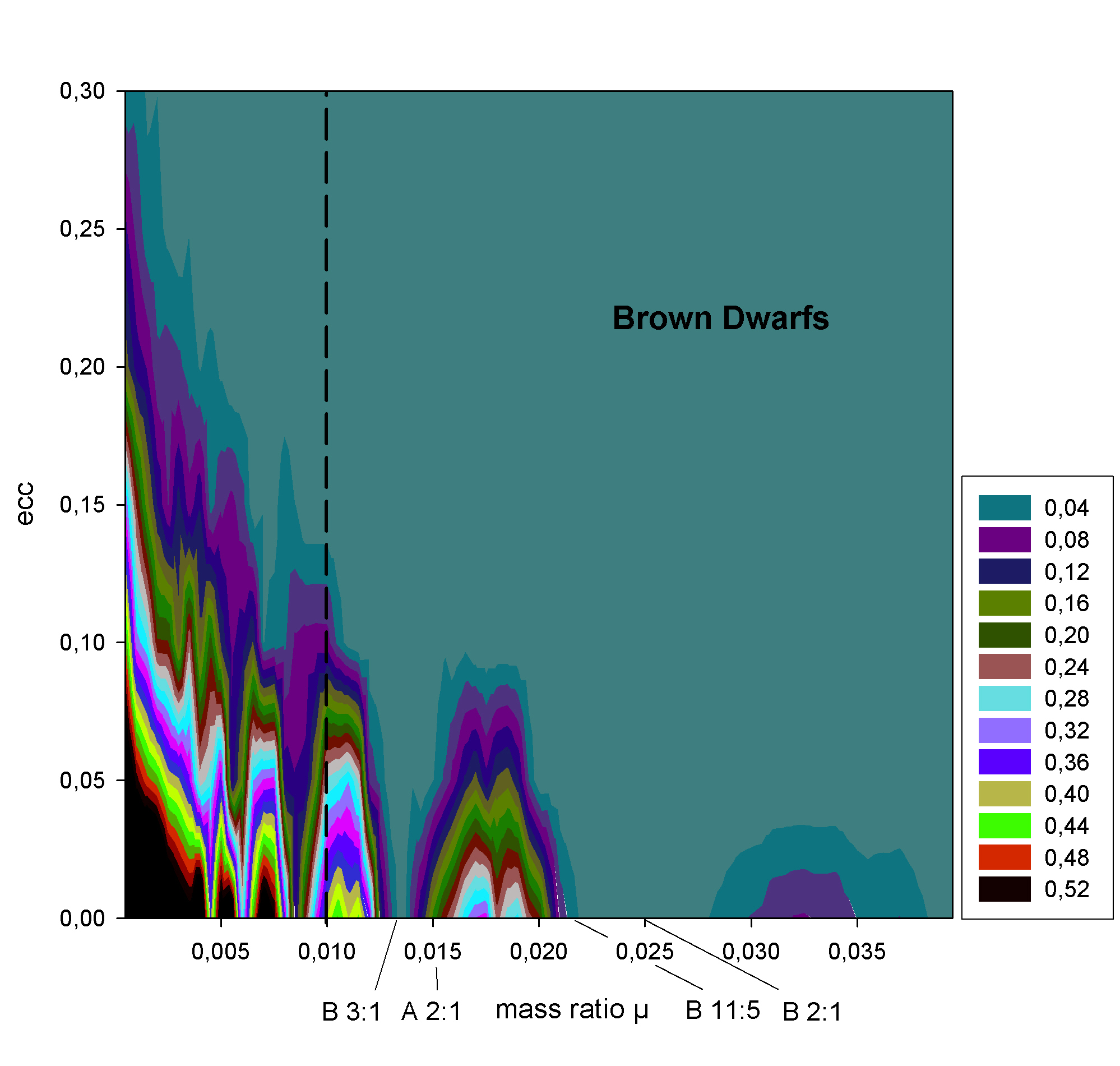
Fig. 3 Fig. 4